Ένα πρόσφατο βίντεο που έγινε viral στα social media προκάλεσε σύγχυση σε χιλιάδες θεατές. Στην απλή αλλά αινιγματική επίδειξη, παρουσιάζονται δύο τροχοί διαφορετικού μεγέθους που κυλούν πάνω σε μια επιφάνεια. Όταν κινούνται ξεχωριστά, ο μεγαλύτερος καλύπτει μεγαλύτερη απόσταση, όπως θα περίμενε κανείς. Όταν όμως ο μικρός τροχός τοποθετείται μέσα στον μεγάλο και οι δύο κυλούν μαζί, συμβαίνει κάτι εντελώς απροσδόκητο: και οι δύο καλύπτουν ακριβώς την ίδια απόσταση σε μία περιστροφή.
Το οπτικό αυτό φαινόμενο φαίνεται να έρχεται σε πλήρη αντίθεση με την κοινή λογική και βασικές γεωμετρικές αρχές. Πώς γίνεται ένας μικρός τροχός, με μικρότερη περιφέρεια, να διανύει την ίδια απόσταση με τον μεγαλύτερο; Το ερώτημα δεν είναι καινούργιο — στην πραγματικότητα, περιγράφηκε για πρώτη φορά πάνω από 2.000 χρόνια πριν και παραμένει ένα από τα πλέον ενδιαφέροντα φιλοσοφικά και επιστημονικά παράδοξα: το Παράδοξο του Τροχού του Αριστοτέλη.
Το παράδοξο: Όταν η γεωμετρία προκαλεί τη λογική
Το λεγόμενο Παράδοξο του Αριστοτέλη βασίζεται σε μια απλή κατασκευή: δύο ομόκεντροι κύκλοι (τροχοί), ένας μεγάλος εξωτερικός και ένας μικρότερος εσωτερικός, είναι στερεά ενωμένοι γύρω από τον ίδιο άξονα. Αν κυλήσει το σύστημα πάνω σε μια επιφάνεια χωρίς ολίσθηση, τότε το χείλος του εξωτερικού τροχού διανύει απόσταση ίση με την περιφέρειά του, όπως αναμένεται.
Το παράδοξο όμως ξεκινά όταν παρατηρήσουμε ότι και ο εσωτερικός τροχός —που είναι συνδεδεμένος αλλά δεν έρχεται σε επαφή με το έδαφος— περιστρέφεται ταυτόχρονα κατά 360 μοίρες. Αυτό θα σήμαινε, σύμφωνα με τα βασικά της γεωμετρίας, ότι κι αυτός διανύει την περιφέρειά του. Αλλά η απόσταση που διανύεται είναι ίση με την περιφέρεια του εξωτερικού τροχού, όχι τη μικρότερη περιφέρεια του εσωτερικού. Πώς γίνεται αυτό χωρίς να υπάρξει παραμόρφωση ή… μαγικά;
Από την Αρχαία Ελλάδα στον Γαλιλαίο
Το αίνιγμα απασχόλησε φιλοσόφους και μαθηματικούς από την εποχή του Αριστοτέλη. Στο έργο Μηχανική, αποδίδεται ήδη η παρατήρηση ότι όταν δύο κύκλοι διαφορετικών μεγεθών είναι ενωμένοι και κυλούν μαζί, ο μικρότερος φαίνεται να παραβιάζει την αναλογική του συμπεριφορά.
Τον 17ο αιώνα, ο Γαλιλαίος επανήλθε στο θέμα, επιχειρώντας μια ευφυή γεωμετρική προσέγγιση: αντικατέστησε τους κύκλους με πολύγωνα, όπως εξάγωνα. Στο σχήμα αυτό, το μεγάλο εξάγωνο κυλά και αφήνει συνεχή επαφή με την επιφάνεια. Το μικρότερο όμως —που δεν αγγίζει το έδαφος— αφήνει ασυνεχή ίχνη, «πηδώντας» μικρά διαστήματα.
Σύμφωνα με τον Γαλιλαίο, το μικρό πολύγωνο δεν χαράζει συνεχή γραμμή αλλά μία με κενά, τα οποία αυξάνονται όσο αυξάνονται οι πλευρές. Ακόμη και αν τα πολύγωνα τείνουν σε κύκλους, αυτά τα μικρά «άλματα» παραμένουν. Ο Γαλιλαίος συνέδεσε μάλιστα τη συμπεριφορά αυτή με την υπόθεση ότι η ύλη δεν είναι συνεχής αλλά απαρτίζεται από άτομα, προτείνοντας μια πρώιμη μορφή ατομισμού. Το εσωτερικό ίχνος του μικρού τροχού —είπε— είναι διακεκομμένο, γεμάτο μικροσκοπικά «κενά» που εξηγούν γιατί η διανυθείσα απόσταση φαίνεται ίση με εκείνη του μεγάλου τροχού.
Δείτε αυτή τη δημοσίευση στο Instagram.
Κύλιση ή ολίσθηση; Η φυσική απάντηση
Η σύγχρονη φυσική δίνει μια πιο τεχνική εξήγηση. Το κλειδί βρίσκεται στη διαφορά μεταξύ κύλισης και ολίσθησης.
Ο εξωτερικός τροχός βρίσκεται σε συνεχή επαφή με την επιφάνεια και κυλά χωρίς να γλιστράει. Αυτό σημαίνει ότι κάθε σημείο της περιφέρειάς του ακουμπά στιγμιαία στο έδαφος πριν σηκωθεί και συνεχίσει.
Αντίθετα, ο εσωτερικός τροχός δεν αγγίζει ποτέ το έδαφος. Αν και περιστρέφεται, η κίνησή του δεν είναι αποτέλεσμα κύλισης, αλλά μεταφέρεται από τον εξωτερικό τροχό, ενώ παράλληλα ολισθαίνει στο εσωτερικό του. Έτσι εξηγείται γιατί φαίνεται να διανύει απόσταση μεγαλύτερη από την περιφέρειά του: η περιστροφή του δεν συνοδεύεται από αντίστοιχη μετατόπιση, όπως συμβαίνει με έναν ελεύθερα κινούμενο τροχό.
Για να το φανταστεί κανείς πιο απτά, σκεφτείτε δύο νομίσματα, το ένα μικρότερο κολλημένο μέσα στο άλλο. Καθώς το εξωτερικό κυλά στο τραπέζι, το εσωτερικό περιστρέφεται στον αέρα, χωρίς να έχει άμεση επαφή με την επιφάνεια. Αν επιχειρούσαμε να τοποθετήσουμε μία εσωτερική επιφάνεια (π.χ. από πάνω), θα βλέπαμε ότι το μικρό νόμισμα ολισθαίνει πάνω της, όχι κυλά.
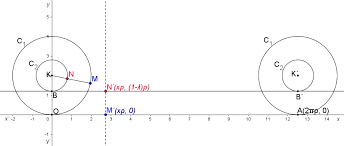
Η γεωμετρία των αριθμών και το μαθηματικό όριο
Η μαθηματική φόρμουλα για την περιφέρεια ενός κύκλου είναι γνωστή:
L = 2πr, όπου r είναι η ακτίνα του κύκλου.
Για έναν τροχό που κυλά χωρίς ολίσθηση, η απόσταση που διανύει σε μία πλήρη περιστροφή είναι ίση με την περιφέρειά του. Άρα:
Ο μεγάλος τροχός, με ακτίνα R, καλύπτει απόσταση 2πR.
Ο μικρός τροχός, με ακτίνα r, θα έπρεπε να καλύψει 2πr, που είναι μικρότερη.
Όμως, όταν ο μικρός είναι συνδεδεμένος μέσα στον μεγάλο, φαίνεται να καλύπτει 2πR, παραβιάζοντας τη γεωμετρική λογική. Η απάντηση είναι ότι δεν κυλάει, αλλά μεταφέρεται και ολισθαίνει ταυτόχρονα, απορρίπτοντας την υπόθεση της «κύλισης χωρίς ολίσθηση» και για τους δύο τροχούς.
Ένα παράδοξο που παραμένει ζωντανό
Το Παράδοξο του Τροχού του Αριστοτέλη δεν είναι ένα απλό μαθηματικό παιχνίδι. Είναι ένα εντυπωσιακό παράδειγμα του πώς η γεωμετρία, η φυσική και η φιλοσοφία μπλέκονται όταν επιχειρούμε να περιγράψουμε την κίνηση στον πραγματικό κόσμο. Αμφισβητεί τη διαισθητική μας κατανόηση της κίνησης και αποκαλύπτει τα όρια της ιδανικής γεωμετρίας, όταν επιχειρεί να περιγράψει τον φυσικό κόσμο.
Και ενώ σήμερα η φυσική εξηγεί το φαινόμενο μέσα από την έννοια της ολίσθησης, το παράδοξο εξακολουθεί να συναρπάζει και να εμπνέει — από τον Αριστοτέλη έως τους χρήστες του TikTok και του YouTube. Δείχνει πως, ακόμα και σε έναν τροχό που κυλά, μπορεί να κρύβεται μια μικρή επανάσταση σκέψης.

